A PDF containing the program can be downloaded here.
Venue
Room 508, Building 2
Sophia University, Tokyo
Friday, March 4
9:45 to 10:00
Opening Remarks
10:00 to 11:00
Linguistics and Some Aspects of its Underlying Dynamics - Part 1
Linguistics and Some Aspects of its Underlying Dynamics
Massimo Piattelli-Palmarini (University of Arizona), Giuseppe Vitiello (University of Salerno)
In recent years, central components of a new approach to linguistics, the Minimalist Program, have come closer to physics. In this talk, an interesting and productive isomorphism is established between minimalist structure, algebraic structures, and many-body field theory opening new avenues of inquiry on the dynamics underlying some central aspects of linguistics. Features such as the unconstrained nature of recursive Merge, the difference between pronounced and un-pronounced copies of elements in a sentence, and the Fibonacci sequence in the syntactic derivation of sentence structures, are shown to be accessible to representation in terms of algebraic formalism.
Linguistics and Some Aspects of its Underlying Dynamics
Massimo Piattelli-Palmarini (University of Arizona), Giuseppe Vitiello (University of Salerno)
In recent years, central components of a new approach to linguistics, the Minimalist Program, have come closer to physics. In this talk, an interesting and productive isomorphism is established between minimalist structure, algebraic structures, and many-body field theory opening new avenues of inquiry on the dynamics underlying some central aspects of linguistics. Features such as the unconstrained nature of recursive Merge, the difference between pronounced and un-pronounced copies of elements in a sentence, and the Fibonacci sequence in the syntactic derivation of sentence structures, are shown to be accessible to representation in terms of algebraic formalism.
Massimo Piattelli-Palmarini (University of Arizona), Giuseppe Vitiello (University of Salerno)
Chair: Roger Martin
11:00 to 11:15 Break
11:15 to 12:15
Linguistics and Some Aspects of its Underlying Dynamics - Part 2
Linguistics and Some Aspects of its Underlying Dynamics
Massimo Piattelli-Palmarini (University of Arizona), Giuseppe Vitiello (University of Salerno)
In recent years, central components of a new approach to linguistics, the Minimalist Program, have come closer to physics. In this talk, an interesting and productive isomorphism is established between minimalist structure, algebraic structures, and many-body field theory opening new avenues of inquiry on the dynamics underlying some central aspects of linguistics. Features such as the unconstrained nature of recursive Merge, the difference between pronounced and un-pronounced copies of elements in a sentence, and the Fibonacci sequence in the syntactic derivation of sentence structures, are shown to be accessible to representation in terms of algebraic formalism.
Linguistics and Some Aspects of its Underlying Dynamics
Massimo Piattelli-Palmarini (University of Arizona), Giuseppe Vitiello (University of Salerno)
In recent years, central components of a new approach to linguistics, the Minimalist Program, have come closer to physics. In this talk, an interesting and productive isomorphism is established between minimalist structure, algebraic structures, and many-body field theory opening new avenues of inquiry on the dynamics underlying some central aspects of linguistics. Features such as the unconstrained nature of recursive Merge, the difference between pronounced and un-pronounced copies of elements in a sentence, and the Fibonacci sequence in the syntactic derivation of sentence structures, are shown to be accessible to representation in terms of algebraic formalism.
Massimo Piattelli-Palmarini (University of Arizona), Giuseppe Vitiello (University of Salerno)
Chair: Roger Martin
12:15 to 13:30 Lunch
13:30 to 14:30
Brain Circuits for Language Processing
Brain Circuits for Language Processing
Kuniyoshi L. Sakai (University of Tokyo)
There is a tacit assumption in neuroscience from the genetic to the systemic level, which holds that the biological foundations of humans are essentially similar to those of nonhuman primates. However, the recent development of linguistics has clarified that human language is radically different from what is known as animal communication. In my talk, I will provide the experimental evidence that the fundamental language processing is indeed specialized in the human brain, focusing particularly on the function of Broca's area. Next, I will summarize new findings on the three syntax-related networks including 19 brain regions, which have been recently identified by our functional connectivity studies. For 21 patients with a left frontal glioma, we observed that almost all of the functional connectivity exhibited chaotic changes in the agrammatic patients. In contrast, some functional connectivity was preserved in an orderly manner in the patients who showed normal performances and activation patterns. More specifically, these latter patients showed normal connectivity between the left fronto-parietal regions, as well as normal connectivity between the left triangular and orbital parts of the left inferior frontal gyrus. Our results indicate that these pathways are most crucial among the syntax-related networks. Both data from the activation patterns and functional connectivity, which are different in temporal domains, should thus be combined to assess any behavioral deficits associated with brain abnormalities. I will further present cortical plasticity for second language (L2) acquisition, such that the activation of language-related regions increases with proficiency improvements at the early stages of L2 acquisition, and that it becomes lower when a higher proficiency in L2 is attained. These results may reflect a more general law of activation changes during language development. The approach to evaluate acquisition processes in terms of not only indirect behavioral changes but direct functional brain changes takes a first step toward a new era in the physics of language.
References:
Kinno, R., Ohta, S., Muragaki, Y., Maruyama, T. & Sakai, K. L.: Left frontal glioma induces functional connectivity changes in syntax-related networks. SpringerPlus 4, 317, 1-6 (2015).
Kinno, R., Ohta, S., Muragaki, Y., Maruyama, T. & Sakai, K. L.: Differential reorganization of three syntax-related networks induced by a left frontal glioma. Brain 137, 1193-1212 (2014).
Ohta, S., Fukui, N. & Sakai, K. L.: Syntactic computation in the human brain: The Degree of Merger as a key factor. PLOS ONE 8, e56230, 1-16 (2013).
Inubushi, T. & Sakai, K. L.: Functional and anatomical correlates of word-, sentence-, and discourse-level integration in sign language. Front. Hum. Neurosci. 7, 681, 1-13 (2013).
Sakai, K. L., Nauchi, A., Tatsuno, Y., Hirano, K., Muraishi, Y., Kimura, M., Bostwick, M. & Yusa, N.: Distinct roles of left inferior frontal regions that explain individual differences in second language acquisition. Hum. Brain Mapp. 30, 2440-2452 (2009).
Sakai, K. L.: Language acquisition and brain development. Science 310, 815-819 (2005).
Brain Circuits for Language Processing
Kuniyoshi L. Sakai (University of Tokyo)
There is a tacit assumption in neuroscience from the genetic to the systemic level, which holds that the biological foundations of humans are essentially similar to those of nonhuman primates. However, the recent development of linguistics has clarified that human language is radically different from what is known as animal communication. In my talk, I will provide the experimental evidence that the fundamental language processing is indeed specialized in the human brain, focusing particularly on the function of Broca's area. Next, I will summarize new findings on the three syntax-related networks including 19 brain regions, which have been recently identified by our functional connectivity studies. For 21 patients with a left frontal glioma, we observed that almost all of the functional connectivity exhibited chaotic changes in the agrammatic patients. In contrast, some functional connectivity was preserved in an orderly manner in the patients who showed normal performances and activation patterns. More specifically, these latter patients showed normal connectivity between the left fronto-parietal regions, as well as normal connectivity between the left triangular and orbital parts of the left inferior frontal gyrus. Our results indicate that these pathways are most crucial among the syntax-related networks. Both data from the activation patterns and functional connectivity, which are different in temporal domains, should thus be combined to assess any behavioral deficits associated with brain abnormalities. I will further present cortical plasticity for second language (L2) acquisition, such that the activation of language-related regions increases with proficiency improvements at the early stages of L2 acquisition, and that it becomes lower when a higher proficiency in L2 is attained. These results may reflect a more general law of activation changes during language development. The approach to evaluate acquisition processes in terms of not only indirect behavioral changes but direct functional brain changes takes a first step toward a new era in the physics of language.
References:
Kinno, R., Ohta, S., Muragaki, Y., Maruyama, T. & Sakai, K. L.: Left frontal glioma induces functional connectivity changes in syntax-related networks. SpringerPlus 4, 317, 1-6 (2015).
Kinno, R., Ohta, S., Muragaki, Y., Maruyama, T. & Sakai, K. L.: Differential reorganization of three syntax-related networks induced by a left frontal glioma. Brain 137, 1193-1212 (2014).
Ohta, S., Fukui, N. & Sakai, K. L.: Syntactic computation in the human brain: The Degree of Merger as a key factor. PLOS ONE 8, e56230, 1-16 (2013).
Inubushi, T. & Sakai, K. L.: Functional and anatomical correlates of word-, sentence-, and discourse-level integration in sign language. Front. Hum. Neurosci. 7, 681, 1-13 (2013).
Sakai, K. L., Nauchi, A., Tatsuno, Y., Hirano, K., Muraishi, Y., Kimura, M., Bostwick, M. & Yusa, N.: Distinct roles of left inferior frontal regions that explain individual differences in second language acquisition. Hum. Brain Mapp. 30, 2440-2452 (2009).
Sakai, K. L.: Language acquisition and brain development. Science 310, 815-819 (2005).
References:
Kinno, R., Ohta, S., Muragaki, Y., Maruyama, T. & Sakai, K. L.: Left frontal glioma induces functional connectivity changes in syntax-related networks. SpringerPlus 4, 317, 1-6 (2015).
Kinno, R., Ohta, S., Muragaki, Y., Maruyama, T. & Sakai, K. L.: Differential reorganization of three syntax-related networks induced by a left frontal glioma. Brain 137, 1193-1212 (2014).
Ohta, S., Fukui, N. & Sakai, K. L.: Syntactic computation in the human brain: The Degree of Merger as a key factor. PLOS ONE 8, e56230, 1-16 (2013).
Inubushi, T. & Sakai, K. L.: Functional and anatomical correlates of word-, sentence-, and discourse-level integration in sign language. Front. Hum. Neurosci. 7, 681, 1-13 (2013).
Sakai, K. L., Nauchi, A., Tatsuno, Y., Hirano, K., Muraishi, Y., Kimura, M., Bostwick, M. & Yusa, N.: Distinct roles of left inferior frontal regions that explain individual differences in second language acquisition. Hum. Brain Mapp. 30, 2440-2452 (2009).
Sakai, K. L.: Language acquisition and brain development. Science 310, 815-819 (2005).
Kuniyoshi L. Sakai (University of Tokyo)
Chair: Masakazu Kuno
14:30 to 14:45 Break
14:45 to 15:45
Merge-Generability as a Crucial Concept in Syntax: An Experimental Study
Merge-Generability as a Crucial Concept in Syntax: An Experimental Study
Shinri Ohta (University of Tokyo), Naoki Fukui (Sophia University), Mihoko Zushi (Kanagawa University), Hiroki Narita (Nihon University), Kuniyoshi L. Sakai (University of Tokyo)
Computational linguistics focused on the Chomsky hierarchy defined on weak generation (the size of the set of output strings). On the other hand, human language does not fit well in the Chomsky hierarchy, i.e., human language is said to be “mildly” context-sensitive. Nested dependencies are frequently observed in human language, while cross-serial dependencies are quite limited. We hypothesized that dependencies are possible only when they are the results from the structures that can be generated by Merge (Merge-generable). Therefore, the most important research topic for both linguistics and neuroscience of language is to elucidate the neural basis of Merge-generability. In the present study, we will first present our recent study with functional magnetic resonance imaging (fMRI), which demonstrated that the complexity of the hierarchical structures generated by Merge modulates cortical activations in the left inferior frontal gyrus (L. IFG), a grammar center in the brain. In the latter part, we will explain our on-going study that tries to examine the Merge-generability of dependencies is crucial for the syntactic computation in the brain. By directly contrasting sentences with Merge-generable and non-Merge-generable dependencies, we found that the main effects of Merge-generability activated the L. IFG, indicating that Merge-generable dependencies—and only Merge-generable dependencies—were handled by the Faculty of language.
References:
Fukui, N.: A Note on weak vs. strong generation in human language. In Á. Gallego & D. Ott eds. 50 Years Later: Reflections on Chomsky's Aspects. Cambridge, MA: MITWPL (2015).
Ohta, S., Fukui, N. & Sakai, K. L.: Syntactic computation in the human brain: The Degree of Merger as a key factor. PLOS ONE 8, e56230, 1-16 (2013).
Ohta, S., Fukui, N. & Sakai, K. L.: Computational principles of syntax in the regions specialized for language: Integrating theoretical linguistics and functional imaging.Front. Behav. Neurosci. 7, 204, 1-13 (2013).
Merge-Generability as a Crucial Concept in Syntax: An Experimental Study
Shinri Ohta (University of Tokyo), Naoki Fukui (Sophia University), Mihoko Zushi (Kanagawa University), Hiroki Narita (Nihon University), Kuniyoshi L. Sakai (University of Tokyo)
Computational linguistics focused on the Chomsky hierarchy defined on weak generation (the size of the set of output strings). On the other hand, human language does not fit well in the Chomsky hierarchy, i.e., human language is said to be “mildly” context-sensitive. Nested dependencies are frequently observed in human language, while cross-serial dependencies are quite limited. We hypothesized that dependencies are possible only when they are the results from the structures that can be generated by Merge (Merge-generable). Therefore, the most important research topic for both linguistics and neuroscience of language is to elucidate the neural basis of Merge-generability. In the present study, we will first present our recent study with functional magnetic resonance imaging (fMRI), which demonstrated that the complexity of the hierarchical structures generated by Merge modulates cortical activations in the left inferior frontal gyrus (L. IFG), a grammar center in the brain. In the latter part, we will explain our on-going study that tries to examine the Merge-generability of dependencies is crucial for the syntactic computation in the brain. By directly contrasting sentences with Merge-generable and non-Merge-generable dependencies, we found that the main effects of Merge-generability activated the L. IFG, indicating that Merge-generable dependencies—and only Merge-generable dependencies—were handled by the Faculty of language.
References:
Fukui, N.: A Note on weak vs. strong generation in human language. In Á. Gallego & D. Ott eds. 50 Years Later: Reflections on Chomsky's Aspects. Cambridge, MA: MITWPL (2015).
Ohta, S., Fukui, N. & Sakai, K. L.: Syntactic computation in the human brain: The Degree of Merger as a key factor. PLOS ONE 8, e56230, 1-16 (2013).
Ohta, S., Fukui, N. & Sakai, K. L.: Computational principles of syntax in the regions specialized for language: Integrating theoretical linguistics and functional imaging.Front. Behav. Neurosci. 7, 204, 1-13 (2013).
References:
Fukui, N.: A Note on weak vs. strong generation in human language. In Á. Gallego & D. Ott eds. 50 Years Later: Reflections on Chomsky's Aspects. Cambridge, MA: MITWPL (2015).
Ohta, S., Fukui, N. & Sakai, K. L.: Syntactic computation in the human brain: The Degree of Merger as a key factor. PLOS ONE 8, e56230, 1-16 (2013).
Ohta, S., Fukui, N. & Sakai, K. L.: Computational principles of syntax in the regions specialized for language: Integrating theoretical linguistics and functional imaging.Front. Behav. Neurosci. 7, 204, 1-13 (2013).
Shinri Ohta (University of Tokyo), Naoki Fukui (Sophia University), Mihoko Zushi (Kanagawa University), Hiroki Narita (Nihon University), Kuniyoshi L. Sakai (University of Tokyo)
Chair: Masakazu Kuno
15:45 to 16:00 Break
16:00 to 17:00
Irreducible Subnets and Random Delays: Limiting the Vocabulary of Neural Information
James Douglas Saddy (University of Reading), Peter Grindrod (Oxford University) [live video]
Chair: Takaomi Kato
17:00 to 17:15 Break
17:15 to 18:15
Emergent Oscillations and Cyclicity: Physical Aspects of Frustrated Cognitive Systems
Emergent Oscillations and Cyclicity: Physical Aspects of Frustrated Cognitive Systems
James Douglas Saddy (University of Reading), Diego Gabriel Krivochen (University of Reading)
This talk will attempt to answer the question “Where does syntax come from?”. This is, of course, a restatement of a very old question; that is, “what is the core type of operation or processes that underlies our cognitive experience?” However, we contend that it is timely to revisit this thorny problem. Recent developments in Mathematics, Physics and Cybernetics have provided a number of sophisticated tools and techniques relevant to answering this question. They are not often brought together largely because they range across a wide landscape of questions and methodologies. Here we will provide a fusion of relevant notions and present what we hope is a kind of answer. We will argue that the ground state of cognitive systems is (a very rich) uncertainty and that an essential part of the dynamics of such uncertain systems necessarily leads to transient simplifications. These simplifications are the stuff of syntax and without them we could not exploit the information embedded in cognitive systems.
The approach assumes that physical principles apply not only to the physiological systems that support cognition but also to the content of cognitive space these systems determine. Here we will not focus on the physiology but the principles we appeal to apply equally to physiological phenomena. Our story depends upon the core notion of dynamic frustration and a further tension between ultrametric and metric spaces. We show that dynamically frustrated systems, as in the case of spin glass, instantiates an ultrametric space (Stein and Newman, 2011; Ramal et al., 1986). As such, they allow for very rich associative fields or manifolds but lack mechanisms that can categorize. However, a general property of dynamical systems is that fields or manifolds can/will interact. The consequences of such interactions are captured in the Center Manifold Theorem (CMT henceforth) which tells us that the intersection of manifolds leads to the creation of a new manifold that is of lower dimensionality and which combines the core dynamics of the intersecting higher dimensional manifolds (Carr, 2006). This is the first core observation, a dynamically frustrated system under conditions found in biologically instantiated systems, will necessarily manifest oscillations between higher and lower dimensionalities and hence between higher and lower entropies. The second core observation is that, while a dynamically frustrated system expresses an ultrametric space, the consequence of the intersection of manifolds in that space, following from the center manifold theorem, is to impose metrical structure onto the lower dimensional, lower entropy offspring. Thus in a dynamically frustrated system we have an engine that necessarily delivers oscillatory behaviour, a very good thing from the neurophysiological point of view (see, e.g., Poeppel et al., 2015), and also moves between ultrametric and metric spaces, quite useful from the information processing point of view (due to the fact that the oscillations provide a built in mechanism that can update the associative manifolds).
Emergent Oscillations and Cyclicity: Physical Aspects of Frustrated Cognitive Systems
James Douglas Saddy (University of Reading), Diego Gabriel Krivochen (University of Reading)
This talk will attempt to answer the question “Where does syntax come from?”. This is, of course, a restatement of a very old question; that is, “what is the core type of operation or processes that underlies our cognitive experience?” However, we contend that it is timely to revisit this thorny problem. Recent developments in Mathematics, Physics and Cybernetics have provided a number of sophisticated tools and techniques relevant to answering this question. They are not often brought together largely because they range across a wide landscape of questions and methodologies. Here we will provide a fusion of relevant notions and present what we hope is a kind of answer. We will argue that the ground state of cognitive systems is (a very rich) uncertainty and that an essential part of the dynamics of such uncertain systems necessarily leads to transient simplifications. These simplifications are the stuff of syntax and without them we could not exploit the information embedded in cognitive systems.
The approach assumes that physical principles apply not only to the physiological systems that support cognition but also to the content of cognitive space these systems determine. Here we will not focus on the physiology but the principles we appeal to apply equally to physiological phenomena. Our story depends upon the core notion of dynamic frustration and a further tension between ultrametric and metric spaces. We show that dynamically frustrated systems, as in the case of spin glass, instantiates an ultrametric space (Stein and Newman, 2011; Ramal et al., 1986). As such, they allow for very rich associative fields or manifolds but lack mechanisms that can categorize. However, a general property of dynamical systems is that fields or manifolds can/will interact. The consequences of such interactions are captured in the Center Manifold Theorem (CMT henceforth) which tells us that the intersection of manifolds leads to the creation of a new manifold that is of lower dimensionality and which combines the core dynamics of the intersecting higher dimensional manifolds (Carr, 2006). This is the first core observation, a dynamically frustrated system under conditions found in biologically instantiated systems, will necessarily manifest oscillations between higher and lower dimensionalities and hence between higher and lower entropies. The second core observation is that, while a dynamically frustrated system expresses an ultrametric space, the consequence of the intersection of manifolds in that space, following from the center manifold theorem, is to impose metrical structure onto the lower dimensional, lower entropy offspring. Thus in a dynamically frustrated system we have an engine that necessarily delivers oscillatory behaviour, a very good thing from the neurophysiological point of view (see, e.g., Poeppel et al., 2015), and also moves between ultrametric and metric spaces, quite useful from the information processing point of view (due to the fact that the oscillations provide a built in mechanism that can update the associative manifolds).
The approach assumes that physical principles apply not only to the physiological systems that support cognition but also to the content of cognitive space these systems determine. Here we will not focus on the physiology but the principles we appeal to apply equally to physiological phenomena. Our story depends upon the core notion of dynamic frustration and a further tension between ultrametric and metric spaces. We show that dynamically frustrated systems, as in the case of spin glass, instantiates an ultrametric space (Stein and Newman, 2011; Ramal et al., 1986). As such, they allow for very rich associative fields or manifolds but lack mechanisms that can categorize. However, a general property of dynamical systems is that fields or manifolds can/will interact. The consequences of such interactions are captured in the Center Manifold Theorem (CMT henceforth) which tells us that the intersection of manifolds leads to the creation of a new manifold that is of lower dimensionality and which combines the core dynamics of the intersecting higher dimensional manifolds (Carr, 2006). This is the first core observation, a dynamically frustrated system under conditions found in biologically instantiated systems, will necessarily manifest oscillations between higher and lower dimensionalities and hence between higher and lower entropies. The second core observation is that, while a dynamically frustrated system expresses an ultrametric space, the consequence of the intersection of manifolds in that space, following from the center manifold theorem, is to impose metrical structure onto the lower dimensional, lower entropy offspring. Thus in a dynamically frustrated system we have an engine that necessarily delivers oscillatory behaviour, a very good thing from the neurophysiological point of view (see, e.g., Poeppel et al., 2015), and also moves between ultrametric and metric spaces, quite useful from the information processing point of view (due to the fact that the oscillations provide a built in mechanism that can update the associative manifolds).
James Douglas Saddy (University of Reading), Diego Gabriel Krivochen (University of Reading)
Chair: Takaomi Kato
18:30 to 20:30
Reception (held at Faculty and Staff Dining Room, Sophia University)
[Pre-registration is necessary. (Link to the online pre-registration)]
Saturday, March 5
10:00 to 11:00
Merge α and Superpositioned Labels
Merge α and Superpositioned Labels
Koji Fujita (Kyoto University)
Free and blind application of Merge (Merge α) gives rise to a variety of phrase structures out of the same set of lexical items. Among others, the distinction between what I have called Pot-Merge and Sub-Merge (following P. Greenfield’s seminal work on cognitive development) plays a major role in biological and evolutionary studies of the faculty of language as a human autapomorphy. In this talk I will explore the possibility that this same distinction is also useful in explaining some linguistic phenomena, thereby corroborating this approach on theoretical linguistic grounds, too. For this purpose, I will make a crucial use of Label indeterminacy for a set formed by Sub-Merge, as in {{α X0 Y0 } … }. In such a case, Label of α can be in a state of superposition, oscillating between two (or more) potential values to be fixed at the interfaces. I will suggest that certain linguistic facts, including Japanese direct and indirect passives, variable auxiliary selection patterns, transitivity alternation of verbs and the like, now follow from Label of α in a systematic way.
References:
Chomsky, N. 2015. Problems of projection—extensions. In E. Di Domenico et al. eds. Structures, Strategies and Beyond: Studies in Honour of Adriana Belletti. John Benjamins.
Fujita, K. 2009. A prospect for evolutionary adequacy: Merge and the evolution and development of human language. Biolinguistics 3.
Fujita, K. 2014. Recursive Merge and human language evolution. In T. Roeper & M. Speas eds. Recursion: Complexity in Cognition. Springer.
Fujita, K. 2016. On certain fallacies in evolutionary linguistics and how one can eliminate them. In K. Fujita & C. Boeckx eds. Advances in Biolinguistics: The Human Language Faculty and Its Biological Basis. Routledge.
Greenfield, P.M. 1991. Language, tools, and brain: the ontogeny and phylogeny of hierarchically organized sequential behavior. Behavioral and Brain Sciences 14.
Merge α and Superpositioned Labels
Koji Fujita (Kyoto University)
Free and blind application of Merge (Merge α) gives rise to a variety of phrase structures out of the same set of lexical items. Among others, the distinction between what I have called Pot-Merge and Sub-Merge (following P. Greenfield’s seminal work on cognitive development) plays a major role in biological and evolutionary studies of the faculty of language as a human autapomorphy. In this talk I will explore the possibility that this same distinction is also useful in explaining some linguistic phenomena, thereby corroborating this approach on theoretical linguistic grounds, too. For this purpose, I will make a crucial use of Label indeterminacy for a set formed by Sub-Merge, as in {{α X0 Y0 } … }. In such a case, Label of α can be in a state of superposition, oscillating between two (or more) potential values to be fixed at the interfaces. I will suggest that certain linguistic facts, including Japanese direct and indirect passives, variable auxiliary selection patterns, transitivity alternation of verbs and the like, now follow from Label of α in a systematic way.
References:
Chomsky, N. 2015. Problems of projection—extensions. In E. Di Domenico et al. eds. Structures, Strategies and Beyond: Studies in Honour of Adriana Belletti. John Benjamins.
Fujita, K. 2009. A prospect for evolutionary adequacy: Merge and the evolution and development of human language. Biolinguistics 3.
Fujita, K. 2014. Recursive Merge and human language evolution. In T. Roeper & M. Speas eds. Recursion: Complexity in Cognition. Springer.
Fujita, K. 2016. On certain fallacies in evolutionary linguistics and how one can eliminate them. In K. Fujita & C. Boeckx eds. Advances in Biolinguistics: The Human Language Faculty and Its Biological Basis. Routledge.
Greenfield, P.M. 1991. Language, tools, and brain: the ontogeny and phylogeny of hierarchically organized sequential behavior. Behavioral and Brain Sciences 14.
References:
Chomsky, N. 2015. Problems of projection—extensions. In E. Di Domenico et al. eds. Structures, Strategies and Beyond: Studies in Honour of Adriana Belletti. John Benjamins.
Fujita, K. 2009. A prospect for evolutionary adequacy: Merge and the evolution and development of human language. Biolinguistics 3.
Fujita, K. 2014. Recursive Merge and human language evolution. In T. Roeper & M. Speas eds. Recursion: Complexity in Cognition. Springer.
Fujita, K. 2016. On certain fallacies in evolutionary linguistics and how one can eliminate them. In K. Fujita & C. Boeckx eds. Advances in Biolinguistics: The Human Language Faculty and Its Biological Basis. Routledge.
Greenfield, P.M. 1991. Language, tools, and brain: the ontogeny and phylogeny of hierarchically organized sequential behavior. Behavioral and Brain Sciences 14.
Koji Fujita (Kyoto University)
Chair: Ángel Gallego
11:00 to 11:15 Break
11:15 to 12:15
Queue Left, Stack-Sort Right: Syntactic Structure without Merge
Queue Left, Stack-sort Right: Syntactic Structure without Merge
David P Medeiros (University of Arizona)
“[H]ow can a system such as human language arise in the mind/brain, or for that matter, in the organic world, in which one seems not to find anything like the basic properties of human language? That problem has sometimes been posed as a crisis for the cognitive sciences. The concerns are appropriate, but their locus is misplaced; they are primarily a problem for biology and the brain sciences, which, as currently understood, do not provide any basis for what appear to be fairly well-established conclusions about language.” (Chomsky 1995: 1-2)
"A discontinuity theory is not the same as a special creation theory. No biological phenomenon is without antecedents." (Lenneberg 1967: 234)
Merge seems conceptually indispensable in describing syntactic structures. Merge realizes the ancient intuition that sentences have parts; as an observation about sentences, that seems hard to deny. But Merge also crystallizes a hypothesis about cognition, claiming that syntactic brackets are “in” the relevant mental representations: left and right brackets delimit the boundaries of the nested units we implicitly analyze sentences into. This view brings with it the inherent problem of how headedness is to be realized: it is empirically evident that bracketings are associated with particular elements (the heads of the phrases they bound), but connecting phrases and their heads formally has proven notoriously problematic.
I propose a different understanding of syntactic brackets, rooted in real-time processing: a left bracket marks the recognition of the category of an item and its storage in temporary memory, while a right bracket marks the retrieval of that item and its integration into a rigidly ordered thematic compositional structure. This identification, applied to the universal parsing process I describe, recovers almost exactly identical tree structures to current Merge-based accounts. This is surprising: what we had described with nested containment relations comes for free from algorithmic transduction of one sequence (of morphemes in surface word order) to another (a universal order of composition of those morphemes).
However, the structures generated by these dynamics of parsing are not quite identical to Merge trees. For example, limitations on word order (213-avoidance in thematic domains; Superiority among A-bar fillers) that require extra stipulations in the standard formulation fall out at once from this architecture. The theory also dispenses with the most problematic aspects of Merge-based theory, including linearization, labeling, and derivational ambiguity of non-ambiguous structures – not to mention the “special creation” cognitive operation Merge itself.
Queue Left, Stack-sort Right: Syntactic Structure without Merge
David P Medeiros (University of Arizona)
“[H]ow can a system such as human language arise in the mind/brain, or for that matter, in the organic world, in which one seems not to find anything like the basic properties of human language? That problem has sometimes been posed as a crisis for the cognitive sciences. The concerns are appropriate, but their locus is misplaced; they are primarily a problem for biology and the brain sciences, which, as currently understood, do not provide any basis for what appear to be fairly well-established conclusions about language.” (Chomsky 1995: 1-2)
"A discontinuity theory is not the same as a special creation theory. No biological phenomenon is without antecedents." (Lenneberg 1967: 234)
Merge seems conceptually indispensable in describing syntactic structures. Merge realizes the ancient intuition that sentences have parts; as an observation about sentences, that seems hard to deny. But Merge also crystallizes a hypothesis about cognition, claiming that syntactic brackets are “in” the relevant mental representations: left and right brackets delimit the boundaries of the nested units we implicitly analyze sentences into. This view brings with it the inherent problem of how headedness is to be realized: it is empirically evident that bracketings are associated with particular elements (the heads of the phrases they bound), but connecting phrases and their heads formally has proven notoriously problematic.
I propose a different understanding of syntactic brackets, rooted in real-time processing: a left bracket marks the recognition of the category of an item and its storage in temporary memory, while a right bracket marks the retrieval of that item and its integration into a rigidly ordered thematic compositional structure. This identification, applied to the universal parsing process I describe, recovers almost exactly identical tree structures to current Merge-based accounts. This is surprising: what we had described with nested containment relations comes for free from algorithmic transduction of one sequence (of morphemes in surface word order) to another (a universal order of composition of those morphemes).
However, the structures generated by these dynamics of parsing are not quite identical to Merge trees. For example, limitations on word order (213-avoidance in thematic domains; Superiority among A-bar fillers) that require extra stipulations in the standard formulation fall out at once from this architecture. The theory also dispenses with the most problematic aspects of Merge-based theory, including linearization, labeling, and derivational ambiguity of non-ambiguous structures – not to mention the “special creation” cognitive operation Merge itself.
"A discontinuity theory is not the same as a special creation theory. No biological phenomenon is without antecedents." (Lenneberg 1967: 234)
Merge seems conceptually indispensable in describing syntactic structures. Merge realizes the ancient intuition that sentences have parts; as an observation about sentences, that seems hard to deny. But Merge also crystallizes a hypothesis about cognition, claiming that syntactic brackets are “in” the relevant mental representations: left and right brackets delimit the boundaries of the nested units we implicitly analyze sentences into. This view brings with it the inherent problem of how headedness is to be realized: it is empirically evident that bracketings are associated with particular elements (the heads of the phrases they bound), but connecting phrases and their heads formally has proven notoriously problematic.
I propose a different understanding of syntactic brackets, rooted in real-time processing: a left bracket marks the recognition of the category of an item and its storage in temporary memory, while a right bracket marks the retrieval of that item and its integration into a rigidly ordered thematic compositional structure. This identification, applied to the universal parsing process I describe, recovers almost exactly identical tree structures to current Merge-based accounts. This is surprising: what we had described with nested containment relations comes for free from algorithmic transduction of one sequence (of morphemes in surface word order) to another (a universal order of composition of those morphemes).
However, the structures generated by these dynamics of parsing are not quite identical to Merge trees. For example, limitations on word order (213-avoidance in thematic domains; Superiority among A-bar fillers) that require extra stipulations in the standard formulation fall out at once from this architecture. The theory also dispenses with the most problematic aspects of Merge-based theory, including linearization, labeling, and derivational ambiguity of non-ambiguous structures – not to mention the “special creation” cognitive operation Merge itself.
David P Medeiros (University of Arizona)
Chair: Ángel Gallego
12:15 to 13:30 Lunch Break
13:30 to 14:30
Language Combinatorics as Matrix Mechanics: Conceptual and Empirical Bases
Language Combinatorics as Matrix Mechanics: Conceptual and Empirical Bases
Juan Uriagereka (University of Maryland), Roger Martin (Yokohama National University), Ángel Gallego (Universitat Autònoma de Barcelona)
In this talk (and the following talk), we will propose an analysis of linguistic categories and their possible combinations by way of syntactic Merge in terms of matrix mechanics. We begin by considering Chomsky’s (1974) distinctions for the “parts of speech” in (1).
(1) a. Noun: [+N, -V]
b. Adjective: [+N, +V]
c. Verb: [-N, +V]
d. Adposition: [-N, -V]
To this, we apply the Fundamental Assumption in (2):
(2) a. ±N is represented as ±1
b. ±V is represented as ±i
It is easy to see that this assumption results in vectors as in (3), a minimal extension of which (substituting the vectors for the matrix diagonal) gives us the matrices in (4):
(3) a. [1, -i] b. [1, i] c. [-1, i] d. [-1, -i].
(4) a.  b.
b. 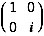 c.
c.  d.
d. 
Matrices such as (4) are very well understood, and under common assumptions concerning the anti-symmetry of Merge can be shown to yield an interesting group. We assume the following representations of two types of Merge:
(5) a. First Merge (for head-complement relations) is represented as matrix multiplication.
b. Elsewhere Merge (for head-specifier relations) is represented as a tensor product.
Interestingly, applying (5a) reflexively (i.e., self-Merge) to any of Chomsky’s matrices interpreted as in (4) yields the same result:
(6) 
(6) is the well-known 3rd Pauli matrix, Z. Further first-mergers among the Chomsky matrices in (4) or the output of these combinations yields three more matrices within the Pauli group:
(7) a.  b.
b.  c.
c. 
We further argue that the Pauli matrices in (8a) and the matrices in (8b), which include the two positive Chomsky matrices and their anti-variants, form a 32-element group in (9), which we tentatively dub the Chomsky-Pauli Group.
(8) a. 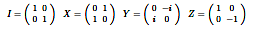
b. 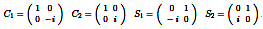
(9) 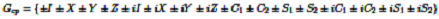
Just as the Chomsky matrices in (4) correspond to lexical categories, we might expect “grammatical categories” to correspond to other elements within the group. Moreover, only certain correspondences between “heads” (lexical items in the group) and “projections” (other elements in the group) yield “endocentric” structures. This is particularly so if we interpret “syntactic label” as in (10):
(10) The “label” of a matrix obtained by Merge is its determinant (= product of the items in the matrix’s main diagonal minus the product of the items in the off-diagonal).
Given this notion of “label,” the only first-mergers that yield “projected” head-complement structures are those in (11).
(11) a. The complement of a noun/adjective is a PP (or a related grammatical projection).
b. The complement of a verb/preposition is an NP (or a related grammatical projection).
We also demonstrate that the only elsewhere-mergers that yield similar symmetries, and can thus said to be “projected” head-specifier structures, are those described in (12).
(12) The specifiers of any type of category is an NP (or a related grammatical projection).
The tensor-product space resulting from multiplying all 32 matrices among themselves also has interesting properties. Among the 1024 tensor-products that the group allows, several matrix combinations are orthogonal. Orthogonal matrices, when added, yield objects with a “dual” character of the sort seen, for instance, in UP and DOWN situations of an electron’s angular momentum – the probability of each relevant state being half – yielding a characteristic “uncertainty” in which the two states are not simultaneously realizable. We have a mathematically identical scenario, this time involving two orthogonal specifiers, which can be said to literally superpose. Thus the behavior of so-called copies in (13) – e.g., the fact that it can be pronounced UP (13b) or DOWN (13c), but not in both configurations (13d) (similar considerations obtain for interpretation) – can be deduced as superposition within this tensor-product space, so long as we define “chains” as in (14).
(13) a. [Armies [appeared [armies ready]]]
b. Armies appeared ready.
c. There appeared armies ready.
d. *Armies appeared armies ready.
(14) A chain C = (A, B) is the sum of two orthogonal tensor-product matrices A and B.
The conditions that yield chain superposition entail the possibility of entanglement of different chains into a super-chain, which is arguably what we see in (15).
(15) a. [Armies tried [armies to [appear [armies ready]]]]
b. Armies tried to appear ready.
Language Combinatorics as Matrix Mechanics: Conceptual and Empirical Bases
Juan Uriagereka (University of Maryland), Roger Martin (Yokohama National University), Ángel Gallego (Universitat Autònoma de Barcelona)
In this talk (and the following talk), we will propose an analysis of linguistic categories and their possible combinations by way of syntactic Merge in terms of matrix mechanics. We begin by considering Chomsky’s (1974) distinctions for the “parts of speech” in (1).
(1) a. Noun: [+N, -V]
b. Adjective: [+N, +V]
c. Verb: [-N, +V]
d. Adposition: [-N, -V]
To this, we apply the Fundamental Assumption in (2):
(2) a. ±N is represented as ±1
b. ±V is represented as ±i
It is easy to see that this assumption results in vectors as in (3), a minimal extension of which (substituting the vectors for the matrix diagonal) gives us the matrices in (4):
(3) a. [1, -i] b. [1, i] c. [-1, i] d. [-1, -i].
(4) a. b.
b. 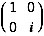 c.
c.  d.
d. 
Matrices such as (4) are very well understood, and under common assumptions concerning the anti-symmetry of Merge can be shown to yield an interesting group. We assume the following representations of two types of Merge:
Interestingly, applying (5a) reflexively (i.e., self-Merge) to any of Chomsky’s matrices interpreted as in (4) yields the same result:
(6)
(6) is the well-known 3rd Pauli matrix, Z. Further first-mergers among the Chomsky matrices in (4) or the output of these combinations yields three more matrices within the Pauli group:
(7) a. b.
b.  c.
c. 
We further argue that the Pauli matrices in (8a) and the matrices in (8b), which include the two positive Chomsky matrices and their anti-variants, form a 32-element group in (9), which we tentatively dub the Chomsky-Pauli Group.
(8) a.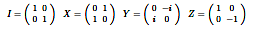
b.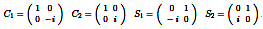
(9)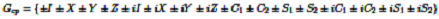
Just as the Chomsky matrices in (4) correspond to lexical categories, we might expect “grammatical categories” to correspond to other elements within the group. Moreover, only certain correspondences between “heads” (lexical items in the group) and “projections” (other elements in the group) yield “endocentric” structures. This is particularly so if we interpret “syntactic label” as in (10):
We also demonstrate that the only elsewhere-mergers that yield similar symmetries, and can thus said to be “projected” head-specifier structures, are those described in (12).
c. There appeared armies ready.
d. *Armies appeared armies ready.
(1) a. Noun: [+N, -V]
b. Adjective: [+N, +V]
c. Verb: [-N, +V]
d. Adposition: [-N, -V]
To this, we apply the Fundamental Assumption in (2):
(2) a. ±N is represented as ±1
b. ±V is represented as ±i
It is easy to see that this assumption results in vectors as in (3), a minimal extension of which (substituting the vectors for the matrix diagonal) gives us the matrices in (4):
(3) a. [1, -i] b. [1, i] c. [-1, i] d. [-1, -i].
(4) a.
 b.
b. 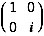 c.
c.  d.
d. 
Matrices such as (4) are very well understood, and under common assumptions concerning the anti-symmetry of Merge can be shown to yield an interesting group. We assume the following representations of two types of Merge:
(5) a. First Merge (for head-complement relations) is represented as matrix multiplication.
b. Elsewhere Merge (for head-specifier relations) is represented as a tensor product.
Interestingly, applying (5a) reflexively (i.e., self-Merge) to any of Chomsky’s matrices interpreted as in (4) yields the same result:
(6)

(6) is the well-known 3rd Pauli matrix, Z. Further first-mergers among the Chomsky matrices in (4) or the output of these combinations yields three more matrices within the Pauli group:
(7) a.
 b.
b.  c.
c. 
We further argue that the Pauli matrices in (8a) and the matrices in (8b), which include the two positive Chomsky matrices and their anti-variants, form a 32-element group in (9), which we tentatively dub the Chomsky-Pauli Group.
(8) a.
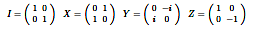
b.
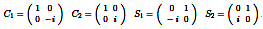
(9)
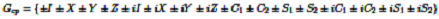
Just as the Chomsky matrices in (4) correspond to lexical categories, we might expect “grammatical categories” to correspond to other elements within the group. Moreover, only certain correspondences between “heads” (lexical items in the group) and “projections” (other elements in the group) yield “endocentric” structures. This is particularly so if we interpret “syntactic label” as in (10):
(10) The “label” of a matrix obtained by Merge is its determinant (= product of the items in the matrix’s main diagonal minus the product of the items in the off-diagonal).
Given this notion of “label,” the only first-mergers that yield “projected” head-complement structures are those in (11).(11) a. The complement of a noun/adjective is a PP (or a related grammatical projection).
b. The complement of a verb/preposition is an NP (or a related grammatical projection).
We also demonstrate that the only elsewhere-mergers that yield similar symmetries, and can thus said to be “projected” head-specifier structures, are those described in (12).
(12) The specifiers of any type of category is an NP (or a related grammatical projection).
The tensor-product space resulting from multiplying all 32 matrices among themselves also has interesting properties. Among the 1024 tensor-products that the group allows, several matrix combinations are orthogonal. Orthogonal matrices, when added, yield objects with a “dual” character of the sort seen, for instance, in UP and DOWN situations of an electron’s angular momentum – the probability of each relevant state being half – yielding a characteristic “uncertainty” in which the two states are not simultaneously realizable. We have a mathematically identical scenario, this time involving two orthogonal specifiers, which can be said to literally superpose. Thus the behavior of so-called copies in (13) – e.g., the fact that it can be pronounced UP (13b) or DOWN (13c), but not in both configurations (13d) (similar considerations obtain for interpretation) – can be deduced as superposition within this tensor-product space, so long as we define “chains” as in (14).(13) a. [Armies [appeared [armies ready]]]
b. Armies appeared ready.c. There appeared armies ready.
d. *Armies appeared armies ready.
(14) A chain C = (A, B) is the sum of two orthogonal tensor-product matrices A and B.
The conditions that yield chain superposition entail the possibility of entanglement of different chains into a super-chain, which is arguably what we see in (15).(15) a. [Armies tried [armies to [appear [armies ready]]]]
b. Armies tried to appear ready.
Juan Uriagereka (University of Maryland) [live video], Roger Martin (Yokohama National University), Ángel Gallego (Universitat Autònoma de Barcelona)
Chair: Hiroki Narita
14:30 to 14:45 Break
14:45 to 15:45
Language Combinatorics as Matrix Mechanics: Mathematical Derivation and Properties
Language Combinatorics as Matrix Mechanics: Mathematical Derivation and Properties
Román Orús (Johannes Gutenberg-Universität), Michael Jarret (University of Maryland)
In this talk we will elaborate on the mathematical details and the analogies to physics of the “Language combinatorics as matrix mechanics” program, introduced in the previous talk. More specifically, here we will motivate and derive the so-called Chomsky-Pauli Group (CPG), a group of 32 matrices of potential relevance in the description of several language processes. In particular, we will show how this group can be derived from very simple initial assumptions (existence of a “name” matrix + reflection symmetry + merge), and how the Pauli group is derived instead of fundamental within this framework (namely, it is a subgroup of the CPG). Other mathematical properties of the CPG will also be explained. Finally, we will present the status of our attempts to build a meaningful Hilbert space from the CPG, in order to describe chains and superchains in linguistics.
Language Combinatorics as Matrix Mechanics: Mathematical Derivation and Properties
Román Orús (Johannes Gutenberg-Universität), Michael Jarret (University of Maryland)
In this talk we will elaborate on the mathematical details and the analogies to physics of the “Language combinatorics as matrix mechanics” program, introduced in the previous talk. More specifically, here we will motivate and derive the so-called Chomsky-Pauli Group (CPG), a group of 32 matrices of potential relevance in the description of several language processes. In particular, we will show how this group can be derived from very simple initial assumptions (existence of a “name” matrix + reflection symmetry + merge), and how the Pauli group is derived instead of fundamental within this framework (namely, it is a subgroup of the CPG). Other mathematical properties of the CPG will also be explained. Finally, we will present the status of our attempts to build a meaningful Hilbert space from the CPG, in order to describe chains and superchains in linguistics.
Román Orús (Johannes Gutenberg-Universität) [live video], Michael Jarret (University of Maryland)
Chair: Hiroki Narita
15:45 to 16:15 Break
16:15 to 17:15
From Geometry and Physics to Computational Linguistics
From Geometry and Physics to Computational Linguistics
Matilde Marcolli (California Institute of Technology)
I will discuss how ideas from Geometry and Statistical Physics can be used to study the structure and evolution of natural languages, within the Principles and Parameters model of syntactic structures. In particular, I will argue that syntactic parameters have a rich geometric structure. The different ways in which they are distributed across different language families can be detected via topological methods. Moreover, sparse distributed memories can detect which
parameters are more easily reconstructible from others. It is known that syntactic parameters of languages
change over time along with language evolution, often as a consequence of the interaction between different languages. I will present a version of spin glass models that is suitable for
quantitative studies of how language interaction affects syntactic parameters and can drive language evolution. The results presented in this talk are based on the papers arXiv:1507.05134,
arXiv:1508.00504, and arXiv:1510.06342.
From Geometry and Physics to Computational Linguistics
Matilde Marcolli (California Institute of Technology)
I will discuss how ideas from Geometry and Statistical Physics can be used to study the structure and evolution of natural languages, within the Principles and Parameters model of syntactic structures. In particular, I will argue that syntactic parameters have a rich geometric structure. The different ways in which they are distributed across different language families can be detected via topological methods. Moreover, sparse distributed memories can detect which
parameters are more easily reconstructible from others. It is known that syntactic parameters of languages
change over time along with language evolution, often as a consequence of the interaction between different languages. I will present a version of spin glass models that is suitable for
quantitative studies of how language interaction affects syntactic parameters and can drive language evolution. The results presented in this talk are based on the papers arXiv:1507.05134,
arXiv:1508.00504, and arXiv:1510.06342.
Matilde Marcolli (California Institute of Technology)
Chair: Michael Jarret
17:15 to 17:30 Break
17:30 to 18:30
Geometric Language to Replace Mathematics and Computer Programming
Geometric Language to Replace Mathematics and Computer Programming
Anirban Bandyopadhyay (National Institute for Materials Science)
We have measured proteins, microfilaments in the neurons and neuron firing at large to identify a new kind of information processing unknown to us in the current neuron firing based approaches. Our experimental finds show that ionic firing in the neuron is not the only route, there is a wireless electromagnetic signalling. If we investigate carefully, the frequency distribution of these signals self-embeds geometric information. Earlier, brain studies never provided us a route to the brain's language processing. We used to consider "bits" as information, and used to fit brain's behavior with what computer scientists developed in artificial intelligence theories with a fitting function. Now, for the first time, we mechanistically unravel the natural language of information processing in the brain.
For us information is not bits. Information is a time cycle, where periodically a few frequencies play sounds at certain intervals. These playing of information holds geometric shapes and we convert every single information in terms of geometric shapes. This particular transition of information definition changes everything. Until now we used to do mathematics by counting, but if we create a language where instead of bits only cycles of frequencies are used then we do not have to worry about counting. We have made an extensive research on replacing various mathematical tools like matrix operation, tensor analysis, solving differential equations using simple geometric transformations. We have kept a special attention to the fact that there is never a geometric transformation that is not possible to implement using structural symmetry breaking in the materials science. Thus, we create the language of physics and then we apply the same for pattern recognition and creating music of images directly to activate senses of human subjects. A pure music to activate the image or taste senses.
Geometric Language to Replace Mathematics and Computer Programming
Anirban Bandyopadhyay (National Institute for Materials Science)
We have measured proteins, microfilaments in the neurons and neuron firing at large to identify a new kind of information processing unknown to us in the current neuron firing based approaches. Our experimental finds show that ionic firing in the neuron is not the only route, there is a wireless electromagnetic signalling. If we investigate carefully, the frequency distribution of these signals self-embeds geometric information. Earlier, brain studies never provided us a route to the brain's language processing. We used to consider "bits" as information, and used to fit brain's behavior with what computer scientists developed in artificial intelligence theories with a fitting function. Now, for the first time, we mechanistically unravel the natural language of information processing in the brain.
For us information is not bits. Information is a time cycle, where periodically a few frequencies play sounds at certain intervals. These playing of information holds geometric shapes and we convert every single information in terms of geometric shapes. This particular transition of information definition changes everything. Until now we used to do mathematics by counting, but if we create a language where instead of bits only cycles of frequencies are used then we do not have to worry about counting. We have made an extensive research on replacing various mathematical tools like matrix operation, tensor analysis, solving differential equations using simple geometric transformations. We have kept a special attention to the fact that there is never a geometric transformation that is not possible to implement using structural symmetry breaking in the materials science. Thus, we create the language of physics and then we apply the same for pattern recognition and creating music of images directly to activate senses of human subjects. A pure music to activate the image or taste senses.
For us information is not bits. Information is a time cycle, where periodically a few frequencies play sounds at certain intervals. These playing of information holds geometric shapes and we convert every single information in terms of geometric shapes. This particular transition of information definition changes everything. Until now we used to do mathematics by counting, but if we create a language where instead of bits only cycles of frequencies are used then we do not have to worry about counting. We have made an extensive research on replacing various mathematical tools like matrix operation, tensor analysis, solving differential equations using simple geometric transformations. We have kept a special attention to the fact that there is never a geometric transformation that is not possible to implement using structural symmetry breaking in the materials science. Thus, we create the language of physics and then we apply the same for pattern recognition and creating music of images directly to activate senses of human subjects. A pure music to activate the image or taste senses.
Anirban Bandyopadhyay (National Institute for Materials Science)
Chair: Michael Jarret
